Jack has 8 identical large cubes and some identical small cubes. He packs all the cubes tightly into a rectangular box such that cubes of the same size are stacked on top of each other. The box is filled to the brim exactly.
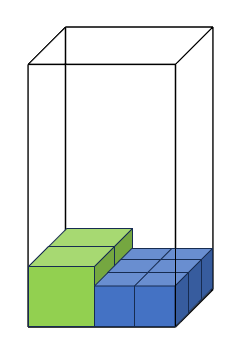
The figure below shows the first layer of cubes packet in the box.
(a) How many small cubes does Jack have ?
(b) The volume of the box is 4032 cm³. The total volume of the 8 large cubes is 3/7 of the volume of the box. What is the length of one edge of the small cube ?
Solution:
Watch the box in 2-D style from above and front view
From top view, we can see the ratio of large cube edge (u) and small cube edge (p) is 3 : 2.
From front view, we need to stack up the large cubes to make four identical levels since there are eight large cubes are packed inside on top of each other. In each level there are two large cubes hence there are four levels of 2 large cubes. It means the height of the box is 4 x u = 4u.
Because the small cubes also stack up till the brim of the box, there will be 6 levels of small cubes. It is shown in the from front view.
==> u : p = 3 : 2 or 6 : 4
(a) There are six levels of small cubes, in each level there are 6 small cubes. So total of small cubes are 6 * 6 = 36.
(b) The total volume of small cubes is 4/7 of the box, which is 4/7 * 4032 = 576 * 4.
Since there are 36 small cubes then each cube volume is (576 * 4) / (9 * 4) = 576 / 9 = 64.
Each cube edge is cubic root of 64 which is 4 cm.
==> 64 = (p * p) * p = (4 * 4) * 4
No comments:
Post a Comment